Specification for a 3D Geometric Type Encoding in Apache Iceberg
Introduction
This specification, named GeoIceberg, details how to add support for a geometric data type in Apache Iceberg to store geospatial data in an Iceberg table. This specification is based on the use of the ISO-19107 standard and the OGC-Simple Feature Access specification.
It is presently a work in progress and hence it is still in a beta version. This work has been initiated in the context of a MSc research work performed at Université Laval, Québec, Canada, by Xavier Malet and under the supervision of Prof. Thierry Badard. This research work aimed at designing a 3D geospatial data lake engine based on the Trino. For any questions or if you want to contribute, please email to Thierry Badard.
This specification was last updated on October 20, 2024.
Context
Apache Iceberg is an open-source data management system designed to store, manage, and version large amounts of structured data.
It offers full support for data evolution and partition management. It works with data formats such as Parquet and ORC.
Iceberg is ideal for storing large amounts of data, allowing for seamless schema evolution and reliable large-scale data management.
However, by default, it does not support geometric data types. This specification proposes an encoding that allows the storage of geometric data type within an Apache Iceberg table.
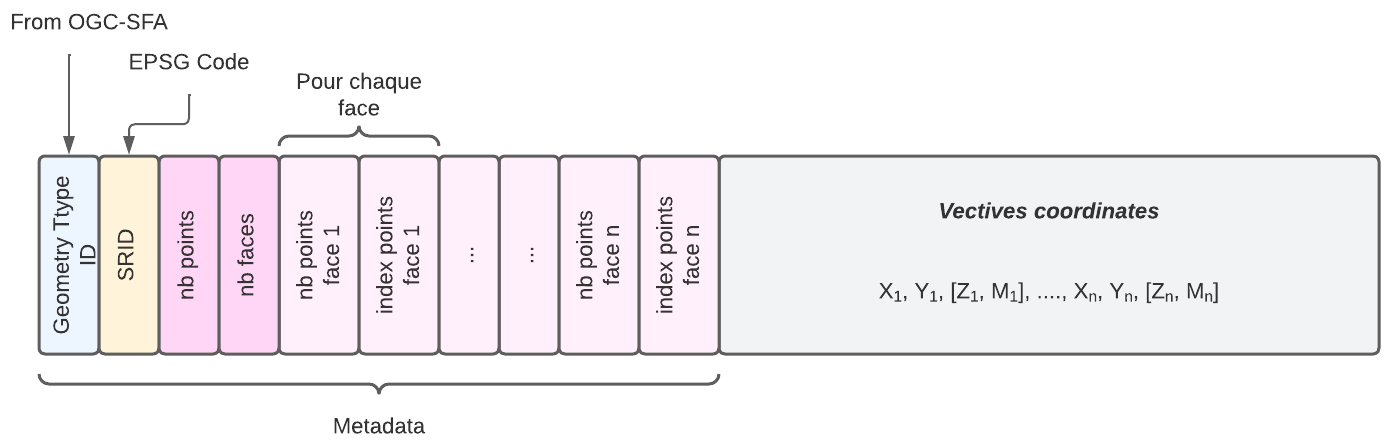
Recognition of Geometric Type in Apache Iceberg
For the geometric data type to be recognized in Apache Iceberg, it is necessary to add mechanisms for recognition, storage, and management of geometric data in:
- The
Schema- Saving the type of geometry used
- The
Partitioning- Allows defining the geospatial partitioning of a table
- The
Manifest- Adding geospatial metrics:
- XMin / XMax / YMin / YMax
- BBox
- Adding geospatial metrics:
- The storage
- Adding geometric data encoders/decoders for storage formats used by
Apache Iceberg, namely:- Parquet
- Avro
- Orc
- Adding geometric data encoders/decoders for storage formats used by
All of this information is disseminated in the metadata files (metadata files)
and in the manifest files.
The data files correspond to storage in Parquet, Orc, Avro type files.
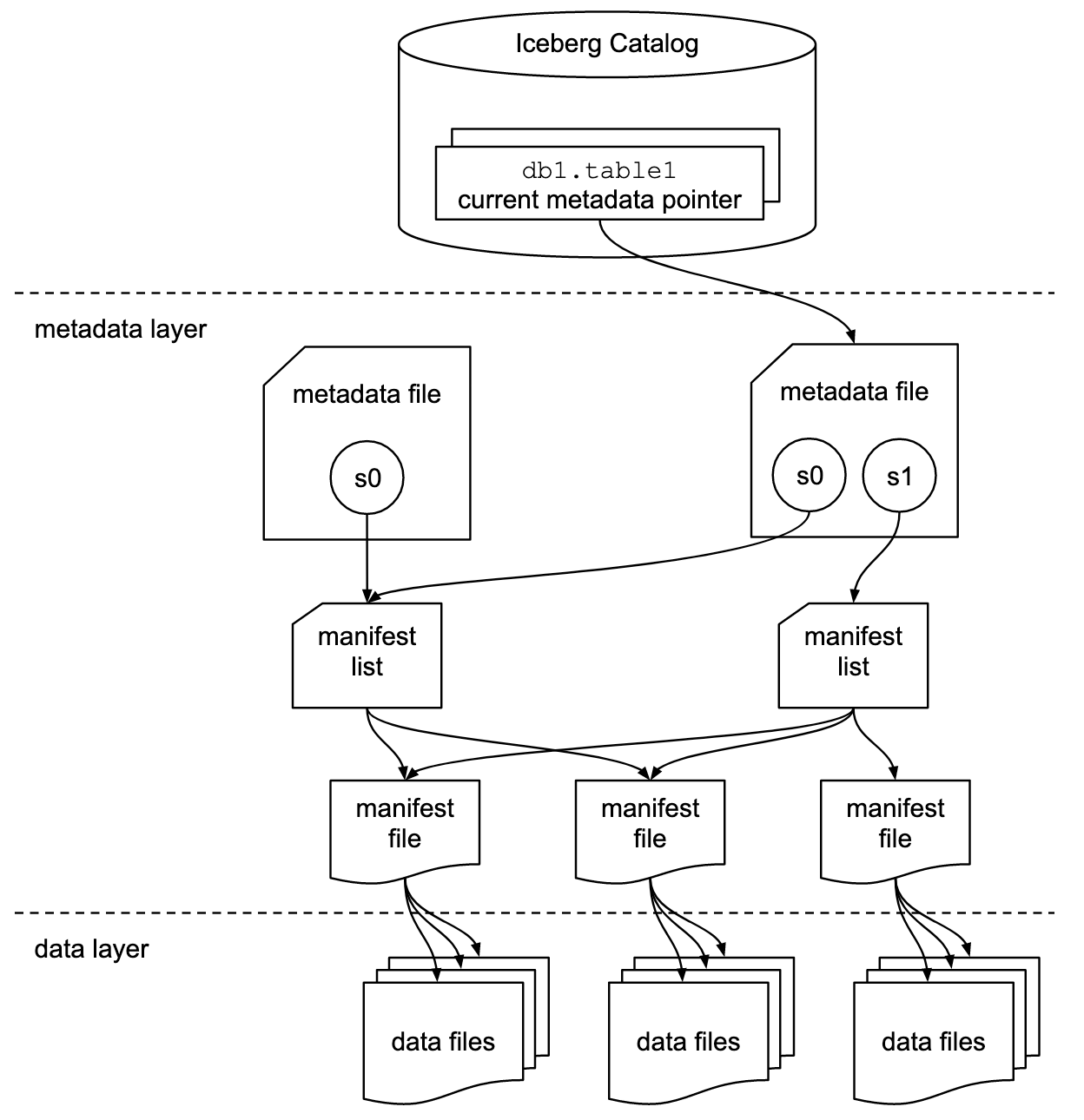
The following sections define:
- The geometric data type in Apache Iceberg
- The use and definition of the geometric data type in the Iceberg schema
- Reading/writing geometries in storage files
- The use of geospatial partitioning
Iceberg Table Schema
To add a geometric data type in Iceberg, it is necessary to define a new geometric data type as defined above.
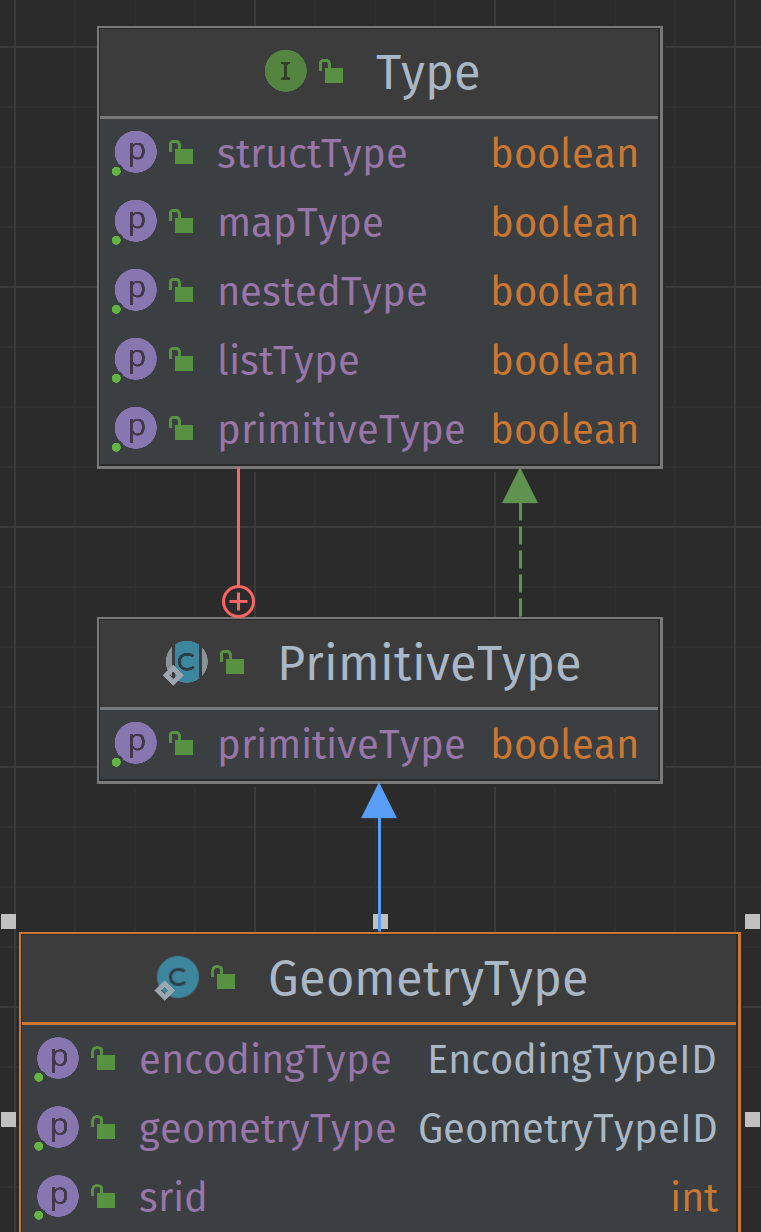
Example schema in pseudo-code:
In Java
StructType SCHEMA = StructType.of(
required(
200, // field id
"geometry", // field name
Types.GeometryType.of("pointzm", 2949, 'WKT') // field type
)
);
In SQL
create table TABLE_NAME (
geom geometry('Pointz',2949,'wkt')
)
This nomenclature corresponds to the one used by PostGIS
Partitions
If partitioning of geometric data is necessary, the partitioning columns should be planned accordingly. For example, geometric data can be partitioned based on geographic region, date, etc.
Several types of geospatial partitioning can be used such as:
For each partitioning, a hash length must be specified to group the different geometries in the same space.
The declaration of geospatial partitioning can be defined as:
GEOPARTITION( TYPE (h2, geohash, ...), GEOMETRIC COL. NAME, HASH LENGTH )
## Example
-- spatial partitioning of type h2 with length 5 on the geometry_col column
GEOPARTITION( 'h2',geometry_col , 5 )
-- spatial partitioning of type geohash with length 5 on the geometry_col column
GEOPARTITION( 'geohash',geometry_col , 5 )
Example schema in pseudo-code:
In SQL (example with the Iceberg - Spark API)
CREATE TABLE prod.db.sample (
id bigint,
geom geometry('pointz',2949,'wkb'))
USING iceberg
PARTITIONED BY (geopartition('geohash',geom, 5))
Indexing
[TO BE COMPLETED] For optimal search performance, it is possible to add spatial indexes to accelerate the search for geometric data.
Reading/Writing Geometric Data
The application using Iceberg must be able to read and write geometric data in the Iceberg table using the appropriate geometric data type.
Geometric data will be stored in a data format compatible with Iceberg, such as Parquet or ORC. The application must support the conversion of geometric data into this format.
Definition of Geometric Data Type
The geometric data type must define:
- The type of geometry used (Point, Line, Polygon, ...).
- The coordinate system (in EPSG format).
- The type of encoding used to serialize/deserialize the geometric object in storage files.
The type definition can be created in SQL or command line with the parameters named above.
Example of type definition:
// Point object with CRS: WGS-84 encoded in WKB
GeometryType("point", 4326, "WKB")
// Point object with CRS: UTM-NAD83 Zone 19 encoded in List
GeometryType("point", 26919, "List")
// Polygon object with CRS: UTM-NAD83 Zone 20 encoded in WKT
GeometryType("polygon", 26920, "WKT")
// PointZ object with CRS: UTM-NAD83 Zone 20 encoded in WKT
GeometryType("pointz", 26920, "WKT")
// PolygonZ object with CRS: UTM-NAD83 Zone 20 encoded in WKT
GeometryType("polygonz", 26920, "WKT")
Supported Geometry Types
The basic objects supported by the OGC-Simple Feature Access specification are:
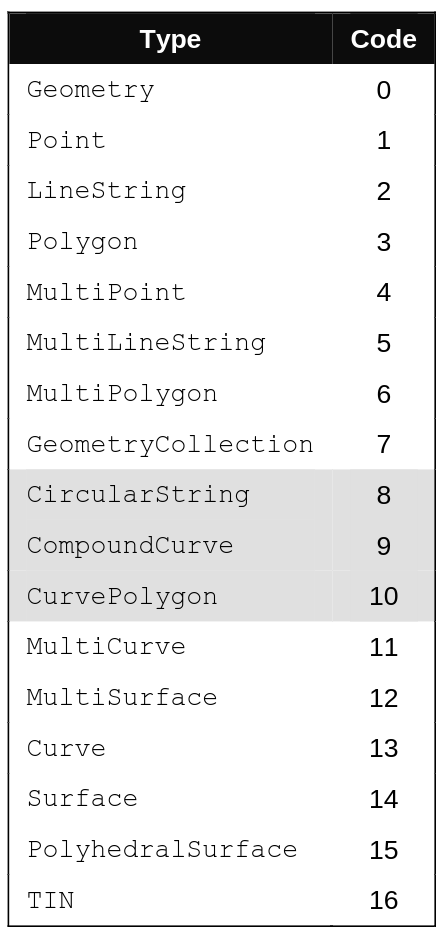
To support 2.5D geometries, simply add the following values
to define objects in XYZ, XYM and XYZM formats
XYZ: 1000XYM: 2000XYZM: 3000
Example:
- PointZ : 1001
- PointM : 2001
-
PointZM: 3001
-
PolygonZ : 1003
- PolygonM : 2003
- PolygonM: 3003
Coordinate System
To identify the coordinate system, the use of EPSG codes is
prioritized.
Geometry Encoding
Among existing encodings, we can name:
-
Well-Known Text (WKT): A human-readable textual representation of geometries. It is used to store geometries in a readable and interpretable way.
-
Well-Known Binary (WKB): A compact binary representation of geometries, making it more efficient for storage and transmission.
-
Tiny Well-Known Binary (TinyWKB): Compact form of WKB used to represent geospatial data efficiently. It is primarily designed to reduce the size of geospatial data when stored or transmitted, while maintaining a simple binary representation.
-
GeoJSON: A JSON format commonly used to represent geospatial objects. It is human-readable and supported by many geospatial libraries and tools.
However, to efficiently store geometric data in files supported by Apache Iceberg, list-based encoding types are preferred for efficiency and performance reasons:
-
Simple List Encoding (SimpleList): This encoding is very similar to WKB encoding. However, instead of being incorporated into a binary representation, the geometry is stored inside an existing container, such as a
ListorArrayobject. This encoding can be difficult to read and decode but is more compact. -
Nested List Encoding (NestedList): Nested list encoding allows storing coordinates inside isolated lists and can simplify the reading/writing process. This type of encoding is partly used in
GeoJSONtype encoding. It is more easily readable by a human but is less compact.
To store geometric objects in Apache Iceberg, the following correspondence can be used:
| Chosen Encoding Type | Apache Iceberg Type Correspondence |
AVRO Correspondence (from Apache Iceberg spec) |
Parquet Correspondence (from Apache Iceberg spec) |
Orc Correspondence (from Apache Iceberg spec) |
|---|---|---|---|---|
| WKT | string |
String | binary | string |
| WKB / TinyWKB | binary |
bytes | binary | binary |
| SimpleList | List( double ) |
array[ double ] | 3-level list | array[ double] |
| NestedList | List( List( double )) |
array[ array[ double ]] | 3-level list | array[ array[ double ]] |
List-based Encoding
This section presents the encoding of geometries using simple lists. This type of encoding has notably been proposed by geoarrow. However, different elements have been added to save the metadata of geometries inside the list.
The following diagram presents the basic structure of simple list encoding for geometries.
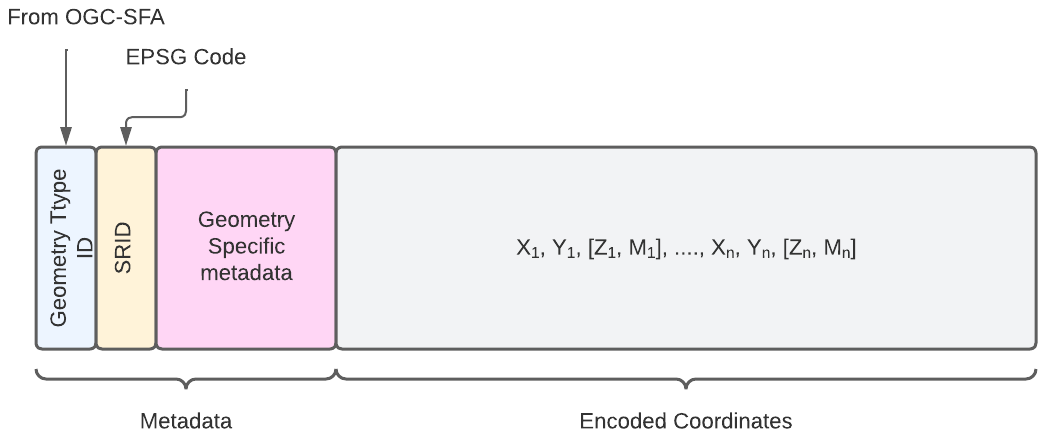
Point Encoding (Point)
- Metadata
- Geometry Type ID:
1 ; 1001; 2001; 3001 - SRID :
int - Geometry Specific Metadata :
None - Encoded Coordinates
- X, Y, Z, M
Example of point encoding
# SRID : 2949
# Point with coordinates : (10,11)
[1, 2949, 10, 11]
# PointZ with coordinates : (10,11, 5)
[1001, 2949, 10, 11, 5]
# PointM with coordinates : (10,11, -15)
[2001, 2949, 10, 11, -15]
# PointZM with coordinates : (10,11, 5, -15)
[3001, 2949, 10, 11, 5, -15]
Line Encoding (LineString)
- Metadata
- Geometry Type ID:
2 ; 1002; 2002; 3002 - SRID :
int - Geometry Specific Metadata :
- dimension (dim):
int: 2 <x< 4 - number of points (nbp):
int: > 1
- dimension (dim):
- Encoded Coordinates
- X1, Y1, Z1, M1, X2, Y2, Z2, M2 ... Xn, Yn, Zn, Mn
Example of Line encoding
# SRID : 2949
# Line with coordinates : [ (0,0), (1,1), (5,5) ]
# | | |
# coord 1 coord 2 coord 3
[2, 2949, 2, 3, 0,0,1,1,5,5]
# ___ ___ ___
# | | | | |
# dim nbp c1 c2 c3
# SRID : 2949
# LineZ with coordinates : [ (0,0,0 ), (1,1,2), (5,5,10) ]
# | | |
# coord 1 coord 2 coord 3
[1002, 2949, 3, 3, 0,0,0,1,1,2,5,5,10]
# _____ _____ _____
# | | | | |
# dim nbp c1 c2 c3
# SRID : 2949
# LineM with coordinates : [ (0,0,10 ), (1,1,11), (5,5,12) ]
# | | |
# coord 1 coord 2 coord 3
[2002, 2949, 3, 3, 0,0,10,1,1,11,5,5,12]
# _____ _____ _____
# | | | | |
# dim nbp c1 c2 c3
# SRID : 2949
# LineZM with coordinates : [ (0,0,1,10 ), (1,1,5,11), (5,5,9,12) ]
# | | |
# coord 1 coord 2 coord 3
[3002, 2949, 4, 3, 0,0,1,10,1,1,5,11,5,5,9,12]
# ________ ________ ________
# | | | | |
# dim nbp c1 c2 c3
Encoding of Multiple Geometries
The encoding of multiple geometries is more complex given that the metadata block becomes more important.
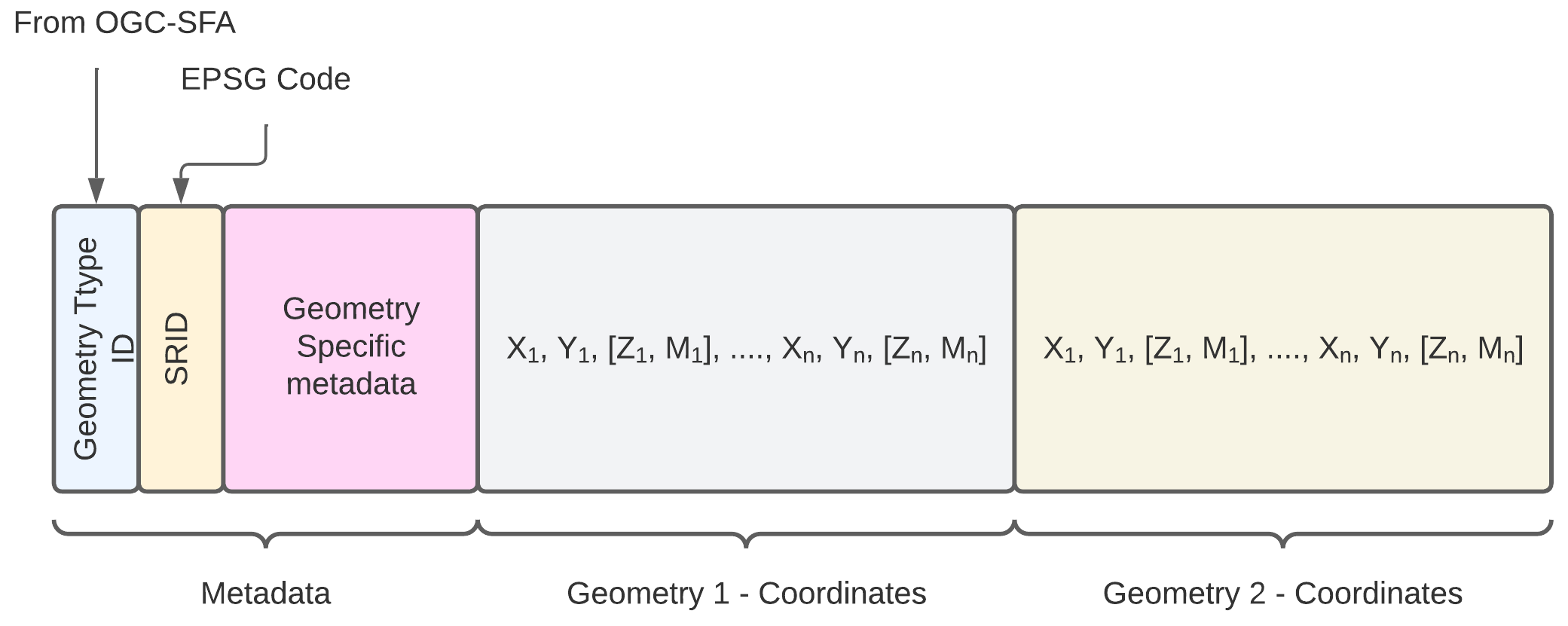
Polygon Encoding (Polygon)
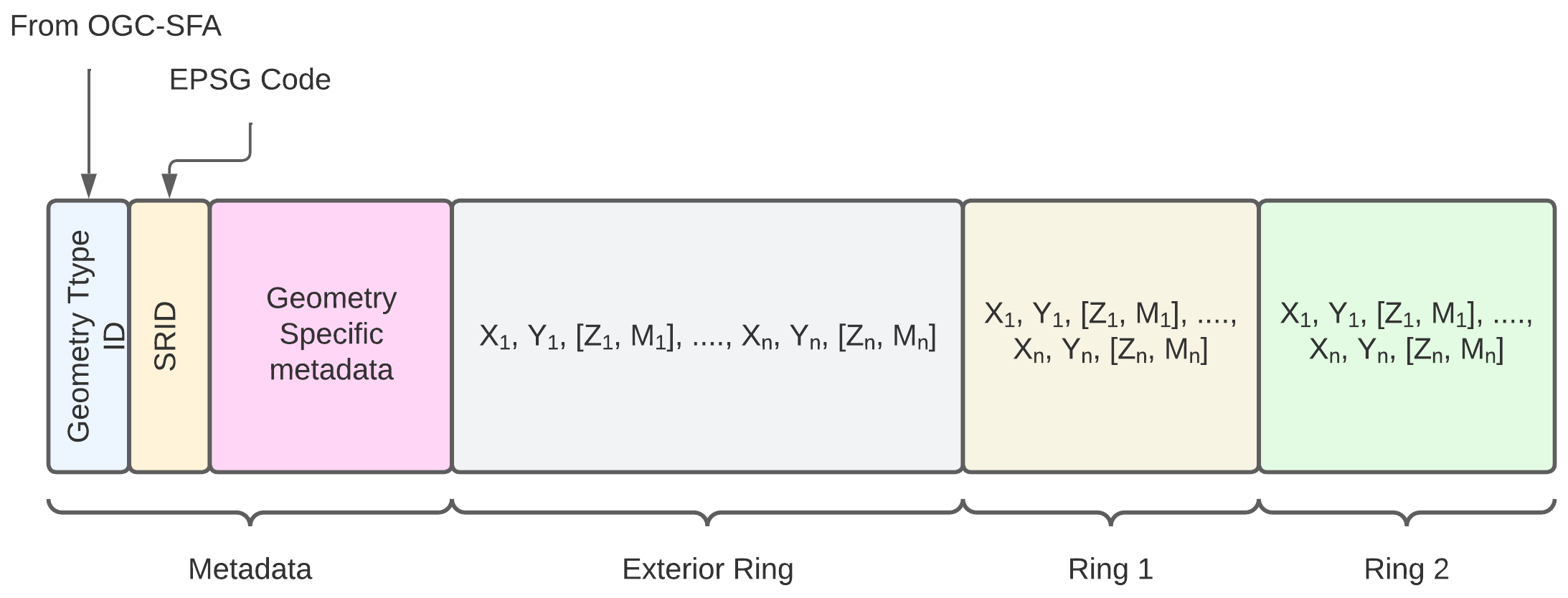
- Metadata
- Geometry Type ID:
3 ; 1003; 2003; 3003 - SRID :
int - Geometry Specific Metadata :
- dimension (dim):
int: 2 <x< 4 - Exterior Ring:
- number of points (nbp):
int: > 1 - Interior Rings
- Ring Number :
int: 0 < X < n - For each ring:
int- number of points (nbp):
int: > 1
- number of points (nbp):
- dimension (dim):
- Encoded Coordinates
- X1, Y1, Z1, M1, X2, Y2, Z2, M2 ... Xn, Yn, Zn, Mn
- For each ring:
- X1ring i, Y1ring i, Z1ring i, M1ring i, X2ring i, Y2ring i, Z2ring i, M2ring i ... Xnring i, Ynring i, Znring i, Mnring i
# SRID: 2949
# Polygon with border: [ (0,0) , (0,5) , (5,5) , (5,0) , (0,0) ]
# Ring 1: A1 [ (1,1) , (1,2) , (2,2) , (2,1) , (1,1) ]
# Ring 2: A2 [ (3,3) , (3,4) , (4,4) , (4,3) , (3,3) ]
# 5,5 5,0
# ┌───────────────────┐
# │ 4,3 4,4 │
# │ ┌────┐ │
# │ │ │ │
# │ │ a2 │ │
# │ 2,1 2,2 └────┘ │
# │ ┌────┐ 3,3 3,4│
# │ │ │ │
# │ │ a1 │ │
# │ └────┘ │
# │ 1,1 1,2 │
# └───────────────────┘
# 0,0 0,5
# Polygon with border: [ (0,0) , (0,5) , (5,5) , (5,0) , (0,0) ]
# without ring
[3, 2949, 2, 5, 0 , 0,0 , 0,5 , 5,5 , 5,0 , 0,0]
# │ │ │ ─┬─ ─┬─ ─┬─ ─┬─ ─┬─
# │ │ │ │ │ │ │ │
# dim │ nr │ │ │ │ │
# nbp c1 c2 c3 c4 c5
# Polygon with border: [ (0,0) , (0,5) , (5,5) , (5,0) , (0,0) ]
# with Ring A1
# Ring 1: A1 [ (1,1) , (1,2) , (2,2) , (2,1) , (1,1) ]
[3, 2949, 2, 5, 1 , 5, 0,0 , 0,5 , 5,5 , 5,0 , 0,0 , 1,1 , 1,2 , 2,2 , 2,1 , 1,1 ]
# │ │ │ │ ─┬─ ─┬─ ─┬─ ─┬─ ─┬─ ─┬─ ─┬─ ─┬─ ─┬─ ─┬─
# │ │ │ │ │ │ │ │ │ │ │ │ │ │
# dim │ nr │ │ Exterior coordinates │ │ │ │ │ │
# │ │ | | | │ │ Ring A1 coordinates │
# nbp │ c1 c2 c3 c4 c5 │ │ │ │ │
# nbp │ │ │ │ │
# ring 1 │ │ │ │ │
# c1 c2 c3 c4 c5
# Polygon with border: [ (0,0) , (0,5) , (5,5) , (5,0) , (0,0) ]
# with Rings A1, A2
# Ring 1: A1 [ (1,1) , (1,2) , (2,2) , (2,1) , (1,1) ]
# Ring 2: A2 [ (3,3) , (3,4) , (4,4) , (4,3) , (3,3) ]
[3, 2949, 2, 5, 2 , 5, 6 , 0,0 , 0,5 , 5,5 , 5,0 , 0,0 , 1,1 , 1,2 , 2,2 , 2,1 , 1,1 , 3,3 , 3,4 , 4,4 , 4,3 , 2.5,3.5 , 3,3 ]
# │ │ │ │ │ ─┬─ ─┬─ ─┬─ ─┬─ ─┬─ ─┬─ ─┬─ ─┬─ ─┬─ ─┬─ ─┬─ ─┬─ ─┬─ ─┬─ ─┬───── ─┬─
# │ │ │ │ │ │ │ │ │ │ │ │ │ │ │ │ │ │ │ │ │
# dim │ nr │ │ │ Exterior coordinates │ │ │ │ │ │ │ │ │ │ │ │
# nbp │ │ | | | │ │ Ring A1 coordinates │ │ Ring A2 coordinates │ │
# nbp ring1 │ c1 c2 c3 c4 c5 │ │ │ │ │ │ │ │ │ │ │
# nbp │ │ │ │ │ c1 c2 c3 c4 c5 c6
# ring2 │ │ │ │ │
# c1 c2 c3 c4 c5
# PolygonZ: [ (0,0,10) , (0,5,10) , (5,5,10) , (5,0,10) , (0,0,10) ]
# without ring
[3, 2949, 3, 5, 0 , 0,0,10 , 0,5,10 , 5,5,10 , 5,0,10 , 0,0,10]
# │ │ │ ──┬─── ──┬─── ──┬─── ──┬─── ──┬───
# │ │ │ │ │ │ │ │
# dim │ nr │ │ │ │ │
# nbp c1 c2 c3 c4 c5
MultiPoints Encoding
- Metadata
- Geometry Type ID:
4 ; 1004; 2004; 3004 - SRID:
int -
Geometry Specific Metadata:
- dimension (dim):
int: 2 <x< 4 - number of points (nbp):
int: > 1
- dimension (dim):
-
Encoded Coordinates
- Xpoint 1, Ypoint 1, Zpoint 1, Mpoint 1
- Xpoint n, Ypoint n, Zpoint n, Mpoint n
# SRID: 2949
# List of points: [ (0,0) , (0,5) , (5,5) , (5,0) ]
# Multipoint
[4, 2949, 2, 4, 0,0 , 0,5 , 5,5 , 5,0]
# │ │ ─┬─ ─┬─ ─┬─ ─┬─
# dim │ p1 p2 p3 p4
# nbp
# MultipointZ
# List of points: [ (0,0,5) , (0,5,14) , (5,5,34) , (5,0, 12) ]
[1004, 2949, 3, 4, 0,0,5 , 0,5,14 , 5,5,34 , 5,0,12]
# │ │ ──┬── ──┬─── ──┬─── ──┬───
# dim │ p1 p2 p3 p4
# nbp
Multilines Encoding
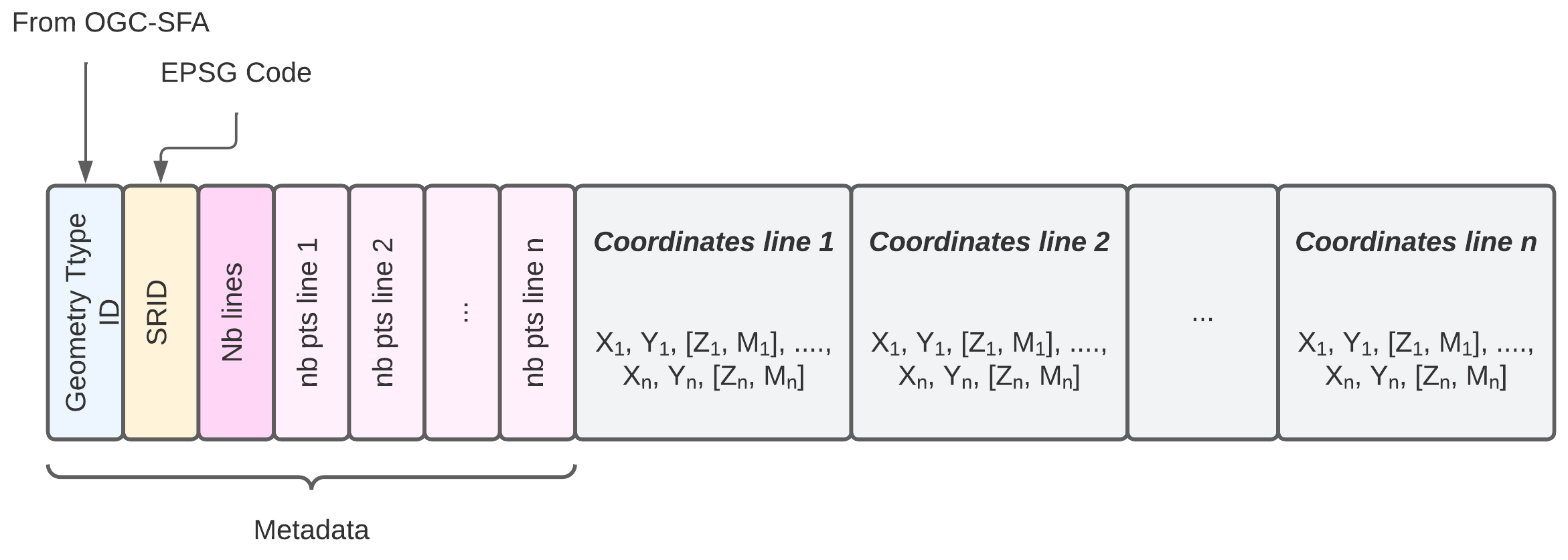
- Metadata
- Geometry Type ID:
5 ; 1005; 2005; 3005 - SRID:
int - Geometry Specific Metadata:
- dimension (dim):
int: 2 <x< 4 - Number of lines:
int: 0 < X < n - For each line:
int- number of points (nbp):
int: > 1
- number of points (nbp):
- dimension (dim):
- Encoded Coordinates
- For each line:
- X1line i, Y1line i, Z1line i, M1line i, X2line i, Y2line i, Z2line i, M2line i ... Xnline i, Ynline i, Znline i, Mnline i
# SRID: 2949
# Line 1: [ (1,1) , (1,2) , (2,2) , (2,1) ]
# Line 2: [ (3,3) , (3,4) , (4,4) ]
# Line 3: [ (0,0) , (0,5) , (5,5) , (5,10) , (10,10) ]
# nbp1 nbp3
# │ │
# │ │
[5, 2949, 2, 3, 4, 3, 5, 1,1,1,2,2,2,2,1 , 3,3,3,4,4,4, 0,0,0,5,5,5,5,10,10,10]
# │ │ │ ──────┬──────── ─────┬───── ───────────┬──────────
# dim │ │ │ │ │
# nb nbp2 x,y line 1 x,y line 3
# lines x,y line 2
# Line 1: [ (1,1,5) , (1,2,12) , (2,2,4) , (2,1,22) ]
# Line 2: [ (3,3,0) , (3,4,12) , (4,4,23) ]
# nbp1
# │
# │
[1005, 2949, 3, 2, 4, 3, 1,1,5,1,2,12,2,2,4,2,1,22 , 3,3,0,3,4,12,4,4,23]
# │ │ │ ──────────┬────────────── ─────────┬─────────
# dim │ │ │ │
# nb nbp2 x,y,z line 1 x,y,z line 2
# lines
MultiPolygons Encoding
TO BE DONE.
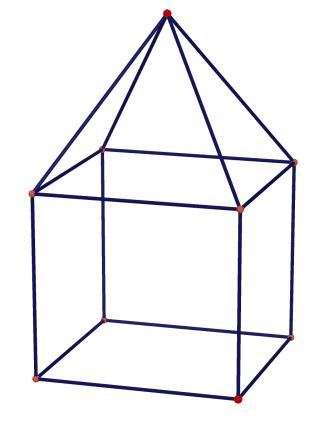
Polyhedra and Solids Encoding (Polyhedral Surface)
Geometrically, a polyhedron can be a 2D/3D structure, and a solid is strictly 3D.
Polyhedra and solids are composed of three important elements:
Faces: basic polygonal geometric shapes (triangle, square, rectangle, ...) that define its exterior.Vertices: set of points composing the differentfacesEdges: straight lines where two faces meet. Each edge connects two vertices and delimits one or more faces.
The figure below presents different basic polyhedra as well as
the elements that compose them (faces, vertices, edges)
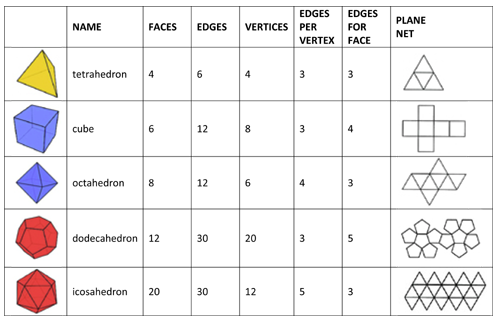
The proposed encoding ignores the storage of edges but stores
the number of vertices, the number of faces, and for each face,
the number of points composing the face as well as the indices of these points
in the coordinate list.
- Metadata
- Geometry Type ID:
15 ; 1015; 2015; 3015 - SRID:
int - Geometry Specific Metadata:
- dimension (dim):
int: 2 <x< 4 - Number of points:
int: 1 < X < n - Number of faces:
int: 1 < X' < n - For each face:
int- number of points (nbp):
int: > 1 - index of points in the list
int:
- number of points (nbp):
- dimension (dim):
- Encoded Coordinates
- All coordinates:
- X1, Y1, Z1, M1, X2, Y2, Z2, M2 ... Xn, Yn, Zn, Mn
Example of tetrahedron encoding
# Tetrahedron encoding
#
# 4 points
#
# 0,0,0
# 1,0,0
# 1,1,0
# 1,1,1
#
# Faces omposition
# 1: 1,2,3
# 2: 1,3,4
# 3: 1,2,4
# 4: 2,3,4
# nb nb pts nb pts
# faces face 2 face 4
# │ │ idx pts │ idx pts
# │ │ │ │ │
# │ │ ──┴── │ ──┴──
[1015, 2949, 3, 4, 4, 3,1,2,3 ,3,1,3,4, 3,1,2,4, 3,2,3,4 , 0,0,0, 1,0,0, 1,1,0, 1,1,1]
# │ │ │ ──┬── │ ───── ──┬── ───── ──┬── ─────
# dim │ │ │idx pts │ │ c2 │ c4
# nb │ │ c1 c3
# points nb pts nb pts
# face 1 face 3
Encoding of a square-based pyramid on a cube
# Tetrahedron encoding
#
# 9 points
#
# index - coordonnées
# Cube
# 1 - 0,0,0
# 2 - 5,0,0
# 3 - 5,5,0
# 4 - 0,5,0
# 5 - 5,5,5
# 6 - 0,5,5
# 7 - 0,0,5
# 8 - 5,0,5
# Top of the Pyramid
# 9 - 2.5,7.5,2.5
#
# Faces omposition
# Cube
# 1,2,3,4
# 1,7,6,4
# 7,8,5,6
# 2,3,5,8
# 1,2,8,7
# Pyramide
# 3,4,9
# 4,6,9
# 5,6,9
# 3,5,9
# nb cube nb pts nb pts
# faces face 2 face 4
# │ │ idx pts │ idx pts
# │ │ │ │ │
# │ │ ──┴──── │ ──┴────
[1015, 2949, 3, 4, 4, 4,1,2,3,4, 4,1,7,6,4, 4,7,8,5,6, 4,2,3,5,8, 4,1,2,8,7,
# │ │ │ ──┬──── │ ──────── │ ────────
# dim │ │ │idx pts │ │
# nb │ │ │
# points cube nb pts cube nb pts cube nb pts
# face 1 face 3 face 5
# Pyramide
3,3,4,9, 3,4,6,9, 3,5,6,9, 3,3,5,9,
# ───── │ ───── │ ───── │ ─────
# └┐ │ │
#nb pts │ │ │
#pyr nb pts │ nb pts
#face 1 pyr nb pts pyr
# face 2 pyr face 4
# face 3
# Vertices
0,0,0, 5,0,0, 5,5,0, 0,5,0, 5,5,5, 0,5,5, 0,0,5, 5,0,5, 2.5,7.5,2.5 ]
#──── ───── ───── ───── ───── ────── ───── ───── ───────────
# c1 c2 c3 c4 c5 c6 c7 c8 c9
Implementations
- Geo3DTrino: a 3D geospatial data lake engine based on Trino.
License
This specification and its translations are released under a Creative Commons Attribution 4.0 International License.